几段唏嘘几世悲欢,可笑我命由我不由天。
矩阵
- 矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合 。
矩阵的定义
- 由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。
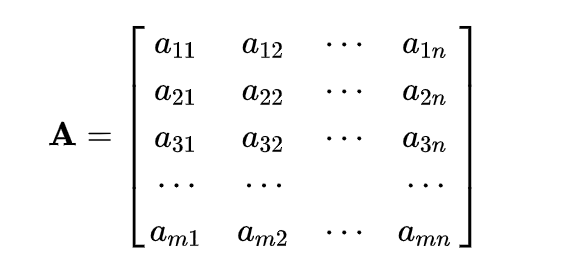
- 这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
- 元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵 。
矩阵的基本运算
- 矩阵的基本运算包括矩阵的加法,减法,数乘,转置,共轭和共轭转置。
- 加法
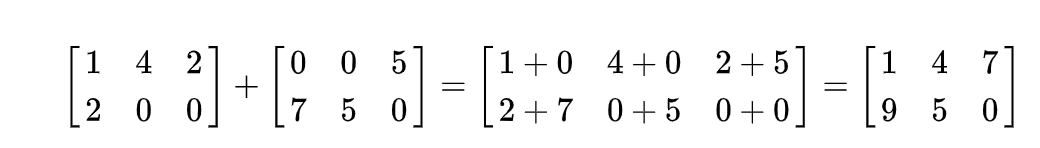
矩阵的加法满足下列运算律(A,B,C都是同型矩阵):
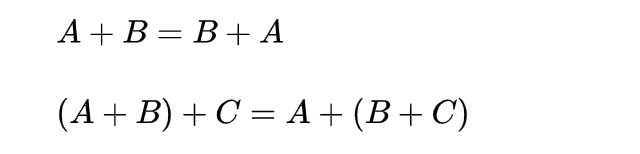
应该注意的是只有同型矩阵之间才可以进行加法
- 减法
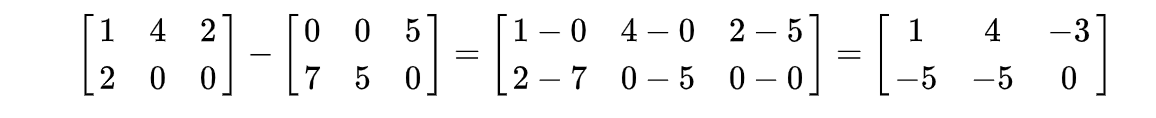
- 数乘
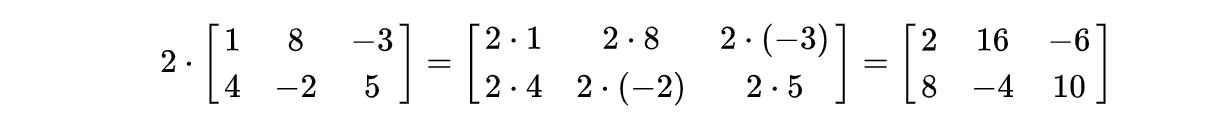
- 矩阵的数乘满足以下运算律:
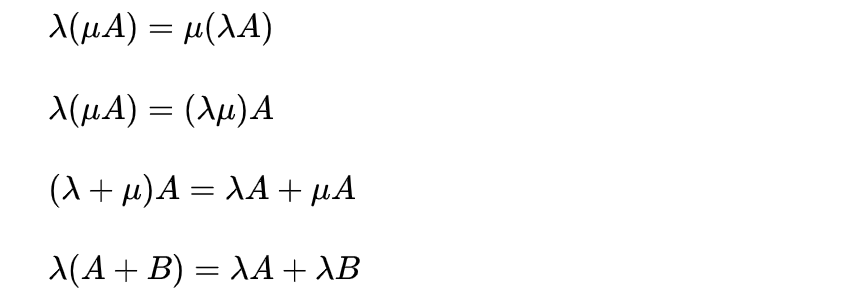
- 矩阵的加减法和矩阵的数乘合称矩阵的线性运
- 转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵,这一过程称为矩阵的转置。
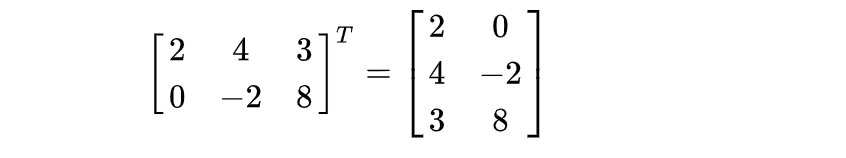
矩阵的转置满足以下运算律
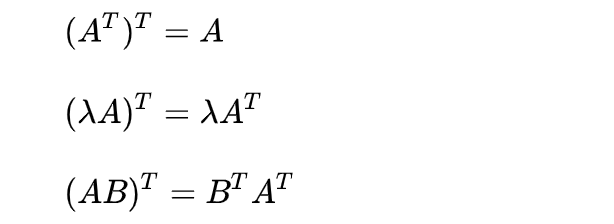
- 共轭
- 一个2×2复数矩阵的共轭(实部不变,虚部取负)
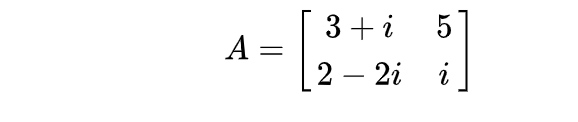
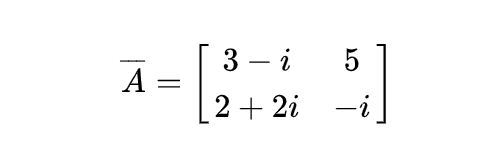
- 共轭转置
- 共轭和转置合在一起
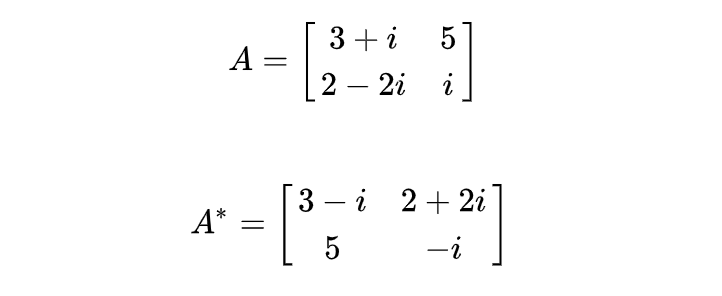
矩阵乘法
- 两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积C是一个m×p矩阵。
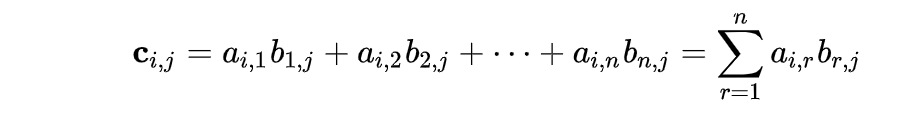
- 例子